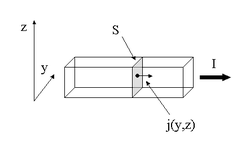
Плотность тока — векторная физическая величина, имеющая смысл силы электрического тока, протекающего через элемент поверхности единичной площади. При равномерном распределении плотности тока и сонаправленности её с нормалью к поверхности, через которую протекает ток, для величины вектора плотности тока выполняется:
j = | j → | = I S , {displaystyle j=|{vec {j}}|={frac {I}{S}},}где I — сила тока через поперечное сечение проводника площадью S (также см. рисунок).
Иногда речь может идти о скалярной плотности тока, в таких случаях под ней подразумевается именно та величина j, которая приведена в формуле.
В общем случае:
I = | ∫ S ( j → , d S → ) | = | ∫ S j n d S | {displaystyle I=|int limits _{S}({vec {j}},{vec {dS}})|=|int limits _{S}j_{n}dS|} ,где j n {displaystyle j_{n}} — нормальная (ортогональная) составляющая вектора плотности тока по отношению к элементу поверхности площадью d S {displaystyle dS} ; вектор d S → {displaystyle {vec {dS}}} — специально вводимый вектор элемента поверхности, ортогональный элементарной площадке и имеющий абсолютную величину, равную её площади, позволяющий записать подынтегральное выражение как обычное скалярное произведение.
Как видим из этого определения, сила тока есть поток вектора плотности тока через некую заданную фиксированную поверхность.
В простейшем предположении, что все носители тока (заряженные частицы) двигаются с одинаковым вектором скорости v → {displaystyle {vec {v}}} и имеют одинаковые заряды q {displaystyle q} (такое предположение может иногда быть приближенно верным; оно позволяет лучше всего понять физический смысл плотности тока), а концентрация их n {displaystyle n} ,
j → = n q v → {displaystyle {vec {j}}=nq{vec {v}}}или
j → = ρ v → , {displaystyle {vec {j}}= ho {vec {v}},}где ρ {displaystyle ho } — плотность заряда этих носителей.
Направление вектора j → {displaystyle {vec {j}}} соответствует направлению вектора скорости v → {displaystyle {vec {v}}} , с которой движутся заряды, создающие ток, если q положительно.
В реальности даже носители одного типа движутся вообще говоря и как правило с различными скоростями. Тогда под v → {displaystyle {vec {v}}} следует понимать среднюю скорость.
В сложных системах (с различными типами носителей заряда, например, в плазме или электролитах)
j → = ∑ i n i q i v → i , {displaystyle {vec {j}}=sum _{i}n_{i}q_{i}{vec {v}}_{i},}то есть вектор плотности тока есть сумма плотностей тока по всем типам подвижных носителей; где n i {displaystyle n_{i}} — концентрация частиц каждого типа, q i {displaystyle q_{i}} — заряд частицы данного типа, v → i {displaystyle {vec {v}}_{i}} — вектор средней скорости частиц этого типа.
Выражение для общего случая может быть записано также через сумму по всем индивидуальным частицам:
j → = ∑ i q i v → i {displaystyle {vec {j}}=sum _{i}q_{i}{vec {v}}_{i}}Сама формула почти совпадает с формулой, приведенной чуть выше, но теперь индекс суммирования i означает не номер типа частицы, а номер каждой индивидуальной частицы, не важно, имеют они одинаковые заряды или разные, при этом концентрации оказываются уже не нужны.
Плотность тока и мощность
Работа, совершаемая электрическим полем над носителями тока, характеризуется, очевидно, плотностью мощности [энергия/(время• объем)]:
w = E → ⋅ j → , {displaystyle w={vec {E}}cdot {vec {j}},}где точкой обозначено скалярное произведение.
Чаще всего эта мощность рассеивается в среду в виде тепла, но вообще говоря она связана с полной работой электрического поля и часть её может переходить в другие виды энергии, например такие, как энергия того или иного вида излучения, механическая работа (особенно — в электродвигателях) и т. д.
Закон Ома
В линейной и изотропной проводящей среде плотность тока связана с напряжённостью электрического поля в данной точке по закону Ома:
j → = σ E → {displaystyle {vec {j}}=sigma {vec {E}}}где σ {displaystyle sigma } — удельная проводимость среды, E → {displaystyle {vec {E}}} — напряжённость электрического поля. Или:
j → = 1 ρ E → , {displaystyle {vec {j}}={frac {1}{ ho }}{vec {E}},}где ρ {displaystyle ho } — удельное сопротивление.
В линейной анизотропной среде имеет место такое же соотношение, однако удельная электропроводность σ {displaystyle sigma } в этом случае, вообще говоря, должна рассматриваться как тензор, а умножение на неё — как умножение вектора на матрицу.
Формула для работы электрического поля (плотности её мощности)
w = E → ⋅ j → , {displaystyle w={vec {E}}cdot {vec {j}},}вместе с законом Ома принимает для изотропной электропроводности вид:
w = σ E 2 = j 2 σ ≡ ρ j 2 , {displaystyle w=sigma E^{2}={frac {j^{2}}{sigma }}equiv ho j^{2},}где σ {displaystyle sigma } и ρ {displaystyle ho } — скаляры, а для анизотропной:
w = E → σ E → = j → ρ j → , {displaystyle w={vec {E}}sigma {vec {E}}={vec {j}} ho {vec {j}},}где подразумевается матричное умножение (справа налево) вектора-столбца на матрицу и на вектор-строку, а тензор σ {displaystyle sigma } и тензор ρ {displaystyle ho } порождают соответствующие квадратичные формы.
4-вектор плотности тока
В теории относительности вводится четырёхвектор плотности тока (4-ток), составленный из объёмной плотности заряда ρ {displaystyle ho } и 3-вектора плотности тока j → : {displaystyle {vec {j}}:}
J μ = ( c ρ , j → ) , {displaystyle J^{mu }=(c ho ,{vec {j}}),}где c {displaystyle c} — скорость света.
4-ток является прямым и естественным обобщением понятия плотности тока на четырёхмерный пространственно-временной формализм и позволяет, в частности, записывать уравнения электродинамики в ковариантном виде.

 Главная
Главная